超几何分布检验

一、超几何分布的定义
超几何分布（Hypergeometric distribution）是统计学上一种离散概率分布。描述了由有限个对象中抽取n个对象，且成功抽出k次指定种类的对象的概率（不放回抽样）。例如，假设总共有N件产品，其中次品有M件。现在从中随机抽取n件做检查，抽到k件次品的概率分布服从超几何分布。

$P(k, N, M, n) = \frac{{M\choose k}\times{{N-M}\choose{n-k}}}{N\choose{n}}$

其中 $k = 0, 1, 2, ..., M$

二、超几何分布检验的用途
超几何分布检验常用来对venn图两个圈overlap的显著性进行检验，用来做富集分析。比如说，检验两个样本的基因集表达是否一致。可以设定P-value保留一致性表达的基因，作为富集基因。

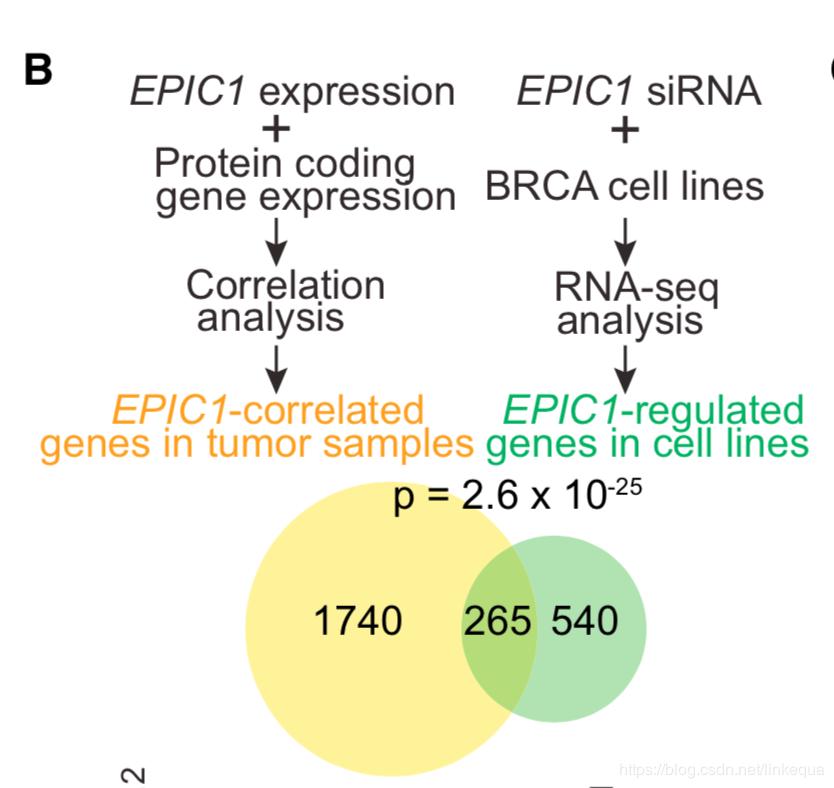
也可以检验基因组中不同功能区域，比如CpG岛，重组热点区域，功能元件区域是否具有显著的Overlap。

三、费歇尔精确检验（Fisher's Test）
Fisher's Test也是一类超几何分布检验，常用来对2x2的列联表进行检验。
举个例子，假设有如下的统计数据：

现在对其进行费歇尔精确检验，有两种提零假设的方法：

1. 对比抽烟组和非抽烟组
   H0：抽烟组得肺癌的概率$p_1$和非抽烟组得肺癌的概率$p_2$相同;
   H1: $p_1$和$p_2$不同（可以分为双侧检验$p_1$ 不等于 $p_2$，或者单侧检验$p_1$>$p_2$ or $p_1$<$p_2$）。
   其中$p_1 =\frac{10}{10+1}$，$p_2=\frac{6}{6+12}$。
   对于上述2x2表，穷尽所有可能为:
   
   ————————————————
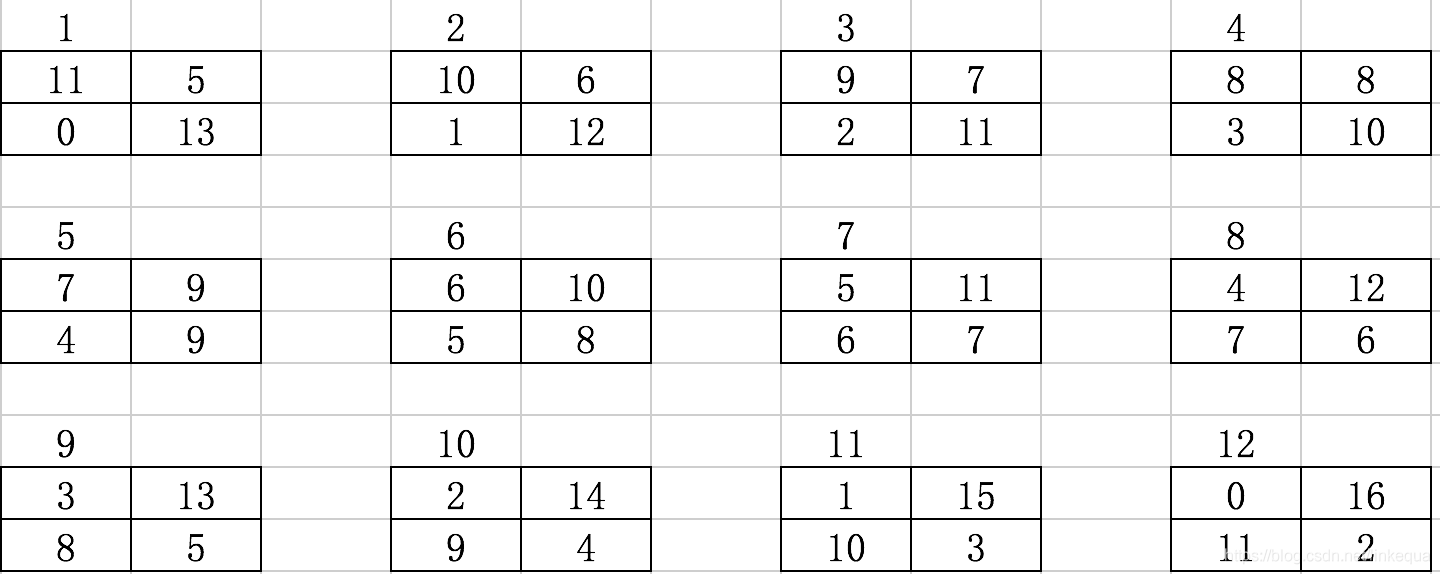
   P1=choose(16, 11)*choose(13,0)/choose(29, 11)=0.00013
   P2=choose(16, 10)*choose(13,1)/choose(29, 11)=0.0030
   P3=choose(16, 9)*choose(13,2)/choose(29, 11)=0.026
   P4=choose(16, 8)*choose(13,3)/choose(29, 11)=0.11
   P5=choose(16, 7)*choose(13,4)/choose(29, 11)=0.24
   P6=choose(16, 6)*choose(13,5)/choose(29, 11)=0.30
   P7=choose(16, 5)*choose(13,6)/choose(29, 11)=0.22
   P8=choose(16, 4)*choose(13,7)/choose(29, 11)=0.090
   P9=choose(16, 3)*choose(13,8)/choose(29, 11)=0.021
   P10=choose(16, 2)*choose(13,9)/choose(29, 11)=0.0025
   P11=choose(16, 1)*choose(13,10)/choose(29, 11)=0.00013
   p12=choose(16, 0)choose(13,11)/choose(29, 11)=2.25e-06
   ————————————————
   很明显对于我们的数据，处在P2的位置，
   对于双侧检验（H1为p 1 ≠ p 2 p1 \neq p2p1 =p2），
   p-value=2(P1+P2)=0.00626
   对于单侧检验（H1为p 1 < p 2 p1 < p2p1<p2），p-value=P2+P3+…+P12=0.99987
   对于单侧检验（H1为p 1 > p 2 p1 > p2p1>p2），
   p-value=P1+P2=0.00313

References:

1. https://zh.wikipedia.org/wiki/%E8%B6%85%E5%87%A0%E4%BD%95%E5%88%86%E5%B8%83
2. https://www.jianshu.com/p/3d01a66e235b
3. https://blog.csdn.net/linkequa/article/details/86491665
4. https://support.minitab.com/zh-cn/minitab/18/help-and-how-to/probability-distributions-and-random-data/supporting-topics/distributions/hypergeometric-distribution/