Hardy-Weinberg平衡

背景：
在研究一个复杂体系时，往往可以考虑从其最简单的模型出发，开始研究。然后再考虑不同的介入因素，丰富模型体系，以适应目标复杂体系的研究。Hardy-Weinberg平衡就是一个这样的理想群体模型，它的定义为：一个族群在理想情况（不受特定的干扰因素影响，如非随机交配、自然选择、族群迁移、突变或群体大小有限），经过多个世代，基因频率与基因型频率会保持恒定并处于稳定的平衡状态。Hardy-Weinberg平衡通常被用来描述群体中等位基因频率和基因型频率的关系。

Hardy-Weinberg平衡的七个假设：

1. 生物是二倍体
2. 只发生有性生殖
3. 世代不重叠
4. 交配是随机的
5. 人口规模无限大
6. 等位基因频率在两性中相等
7. 没有迁移、基因流动、混合、突变或选择

一、随机交配的定义

最简单的群体遗传模型可以从一个没有自然选择、族群迁移、突变的无限群体大小的随机交配群体出发。
随机交配：指群体中每一个成员与另一性别的任何成员都有同等的交配机会。
如果用D、H、R表示群体中相应于AA、Aa、aa的基因型频率，则群体的随机交配类型和频率如下表：

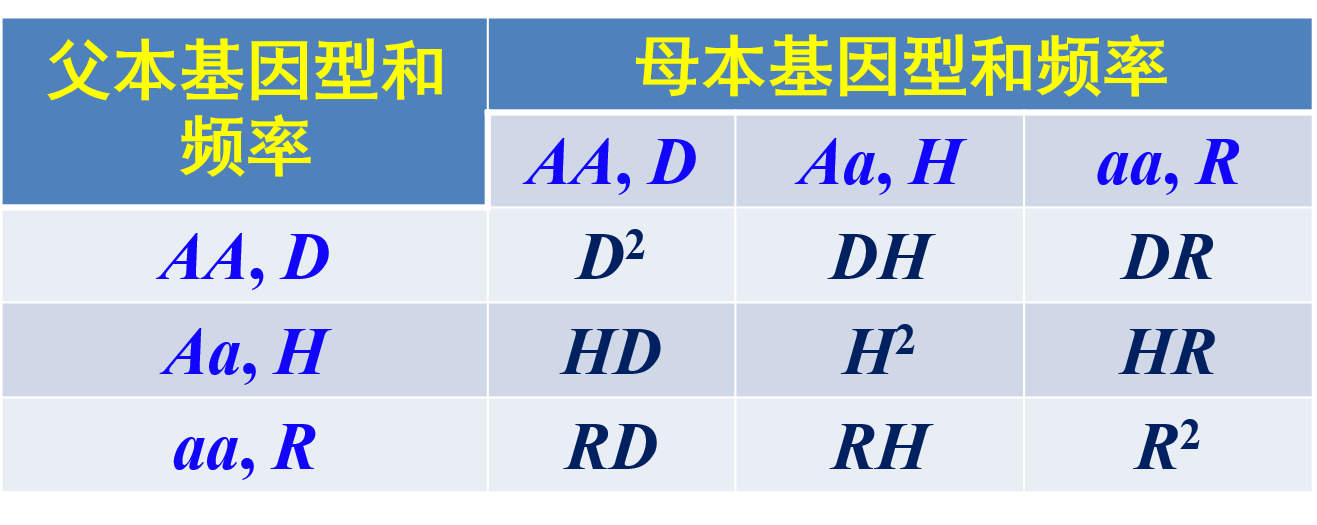
二、Hardy-Weinberg平衡定律
在一个群体中，一个座位上两个等位基因A和a的频率为p和q，三种基因型AA、Aa和aa的频率为D、H和R，如果基因型频率和基因频率满足：
$D=p^2$、$H=2pq$、$R=q^2$，或者说 D、H、R对应于二项式 $(p+q)^2$ 的展开项
则称该群体处于Hardy-Weinberg平衡状态。

1. HWE群体的随机交配后代仍然处于HWE状态
   假设一个随机交配群体中，对于一个等位基因座上的等位基因频率和基因型频率存在这样的关系：
   AA：$D=p^2$、Aa：$H=2pq$、aa：$R=q^2$
   则其后代基因型和基因型频率存在以下关系：
   
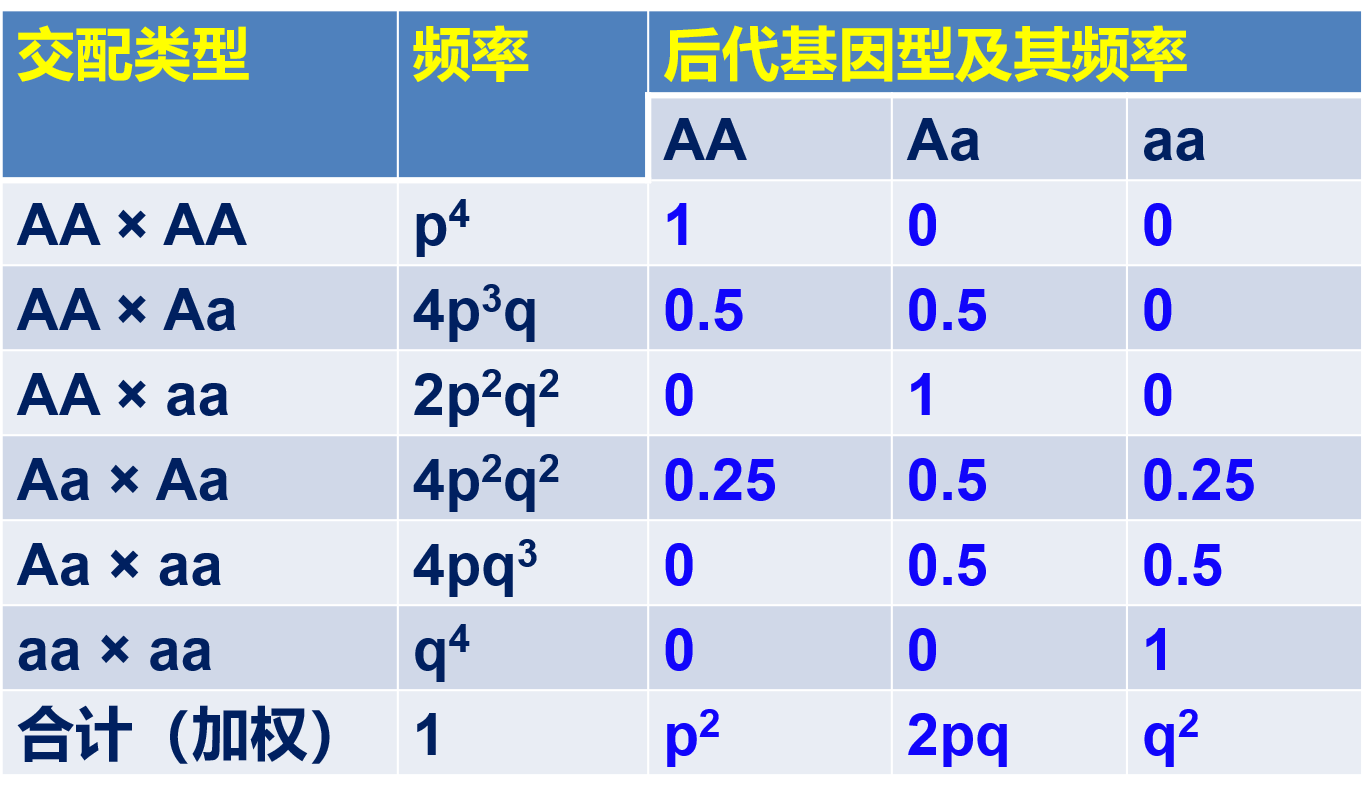
   可以看到，后代各基因型的频率分布仍保持亲代的状态：
   AA：$D=p^2$、Aa：$H=2pq$、aa：$R=q^2$

2. 不管群体的起始频率如何, 只要经过一代随机交配, 群体就达到平衡
   假设一个随机交配群体中，对于一个等位基因座上的等位基因频率和基因型频率存在这样的关系：
   AA: $D$, Aa: $H$, aa: $R$; A: $p=D+0.5H$, a: $q=0.5H+R$
   则其后代基因型和基因型频率存在以下关系：
   
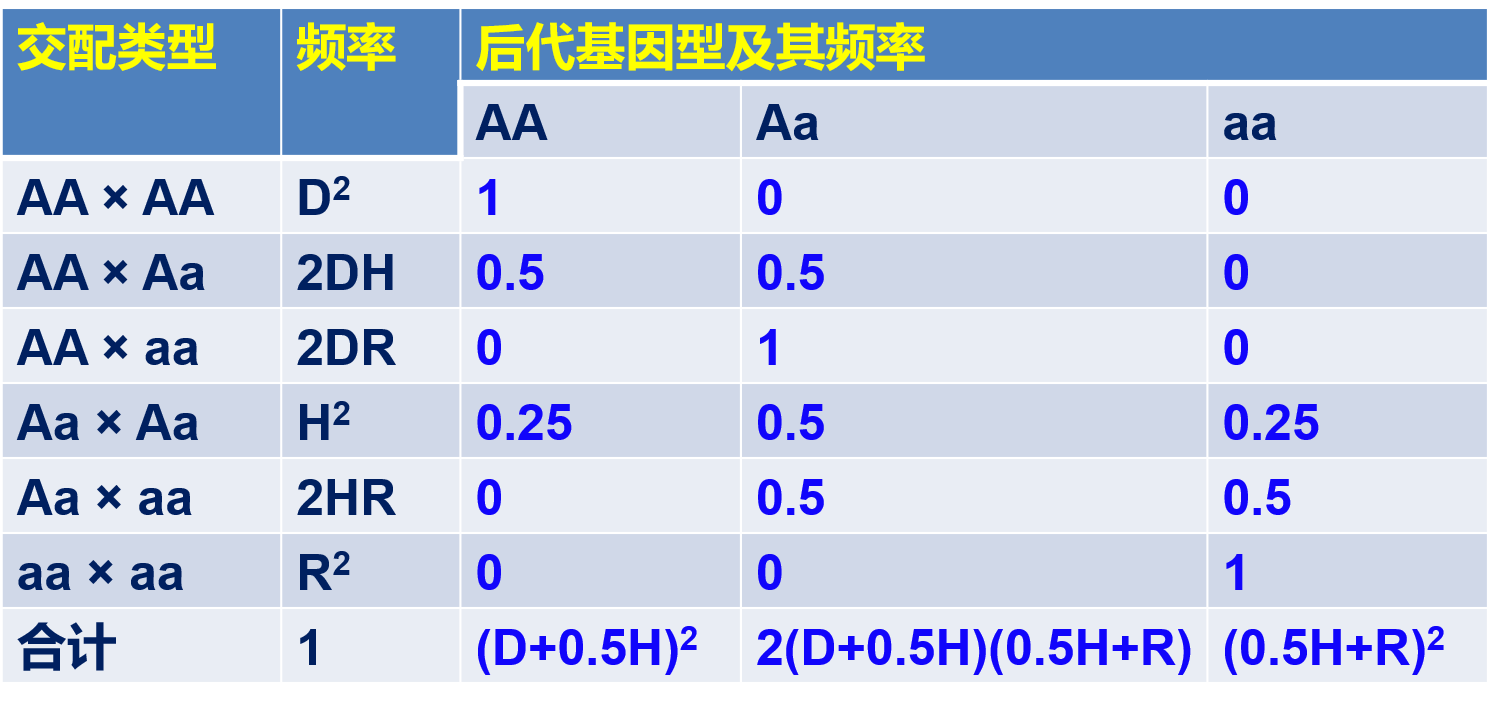
   在随机交配群体中，两个等位基因A和a的频率分别为p和q，如果没有干扰因素，三种基因型AA、Aa、aa的频率总是 p2、2pq、q2，也就是说基因频率和基因型频率将永远保持不变，群体的遗传结构处于一种平衡状态。这个定律是由Hardy和Weinberg在1908年同时发现的，所以一般称为Hardy-Weinberg平衡定律。

三、Hardy-Weinberg平衡群体的性质

1. 在一个平衡群体中，杂合子的频率不会超过0.5，也不可能大于纯合子的频率之和
   杂合子频率H及其相对A等位基因频率p的变化速率为：

$H=2p(1-p)=2p-2p^2$

$\frac{dH}{dp} = 2-4p$

H在$p=0.5$处达到极大值0.5
同理，AA和aa的分布曲线分别为$D=p^2$，$R=(1-p)^2$

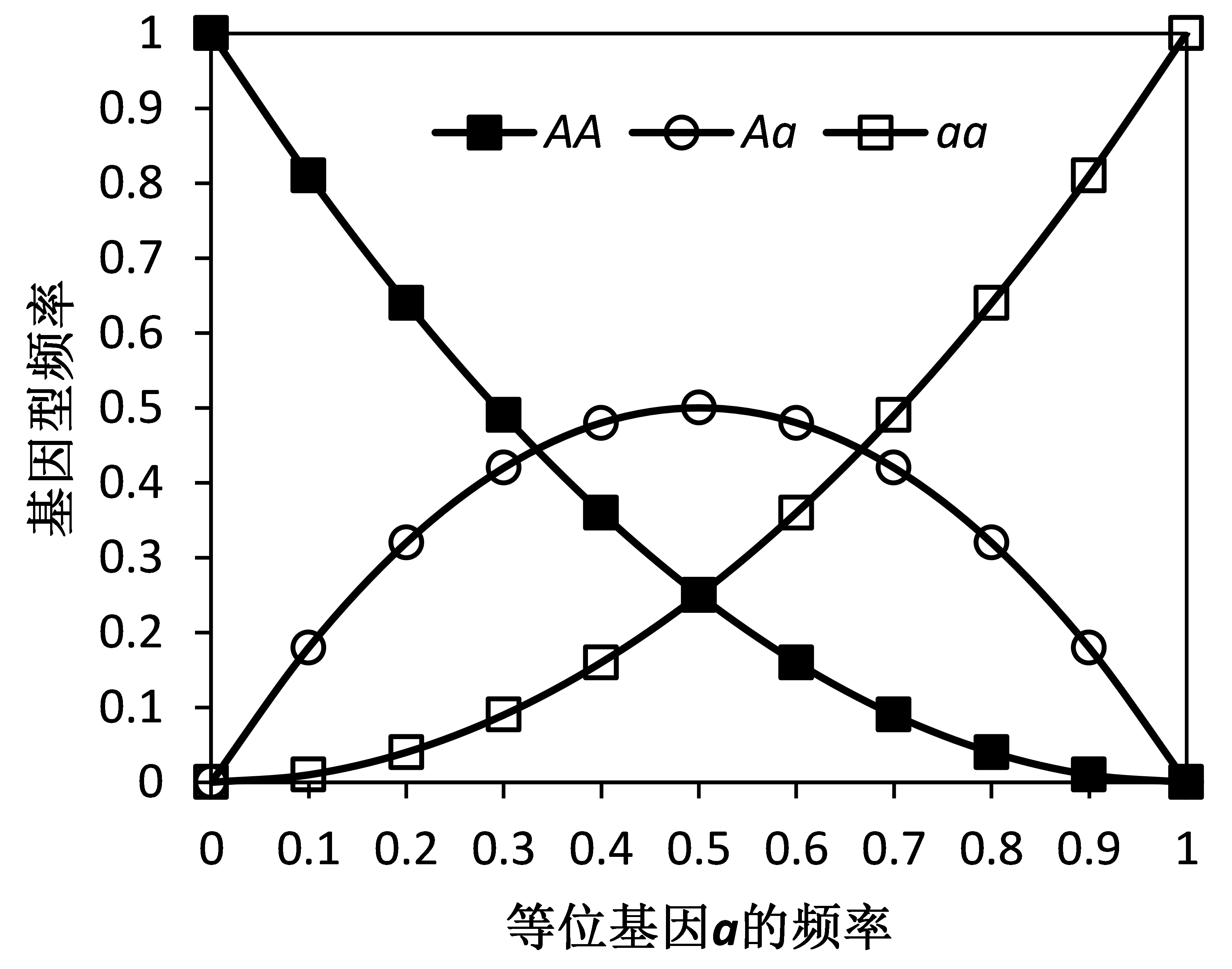
1. 当一个等位基因的频率是另一个的2倍以上时，杂合体频率介于两种纯合体之间
   令 $p/(1-p) >= 2$，则
   $H/D = 2p(1-p) / p^2 = 2(1-p)/p <= 1$
   $H/R = 2p(1-p) / (1-p)^2 = 2p/(1-p) >= 4$
   同理 令 (1-p)/p >= 2，则
   $H/D = 2p(1-p) / p^2 = 2(1-p)/p >= 4$
   $H/R = 2p(1-p) / (1-p)^2 = 2p/(1-p) <= 1$
   也可以来反证，
   令$R <= H <= D$，则有
   $(1-p)^2 <= 2p(1-p) <= p^2$
2. 当一个a基因有很小的频率 (q) 时，该基因大多存在于杂合体中
   杂合型Aa与隐性纯合型aa携带有害基因a的比例为：

$\frac{H}{2R} = \frac{2(1-q)q}{2q^2} = \frac{1}{q}-1$

因此, 对于很小的q, 该比值会非常大

四、Hardy-Weinberg平衡定律的作用

• 测定基因和基因型频率
• 计算隐性基因控制的性状上，正常表型中杂合体（或携带者）的频率。如某种疾病为隐性基因控制，纯合隐性表现症状，杂合体并不表现症状，那么往往需要了解致病基因携带者在正常人群中所占的比重，这便是杂合体所占的频率。设隐性等位基因频率为q。

$\frac{H}{D+H} = \frac{2q(1-q)}{2q(1-q)+(1-q)^2} = \frac{2q}{1+q}$

当q很小时，$\frac{H}{D+H} = \frac{2q}{1+q} \approx{2q}$

五、Hardy-Weinberg平衡的检验
当已知三种基因型的观测个数时，就可知道群体的基因频率和HW平衡时的期望基因型频率。这样可以采用下面的χ2 统计量，测验期望观测值和实际观测值间是否有显著差异。

$\chi^2 = \sum{\frac{(Observed-Expected)^2}{Expected }} \sim \chi^2(df)$

一般来说， $\chi^2$统计量的自由度比分组数少1。但是，如果需要利用观测值估计基因频率，自由度还应该减去独立基因频率的个数。

References:

1. https://en.wikipedia.org/wiki/Hardy%E2%80%93Weinberg_principle
2. https://www.isbreeding.net/teaching/?type=detail&id=14