GWAS原理

GWAS（Genome-Wide Association Study）在遗传学上经常被用来确定与特定疾病或表型相关的全基因组范围内特定遗传变异。

1. GWAS拟解决的问题
GWAS旨在从全基因组范围内定位到和common disease（或者一些常见表型）关联的变异位点。common disease同时受遗传因素和环境因素影响，整体发病率较高，患者群体数目大，而且其遗传因子往往呈现微效，多因子的特点。因此，这种类型疾病的遗传定位往往需要庞大的人群队列进行研究。

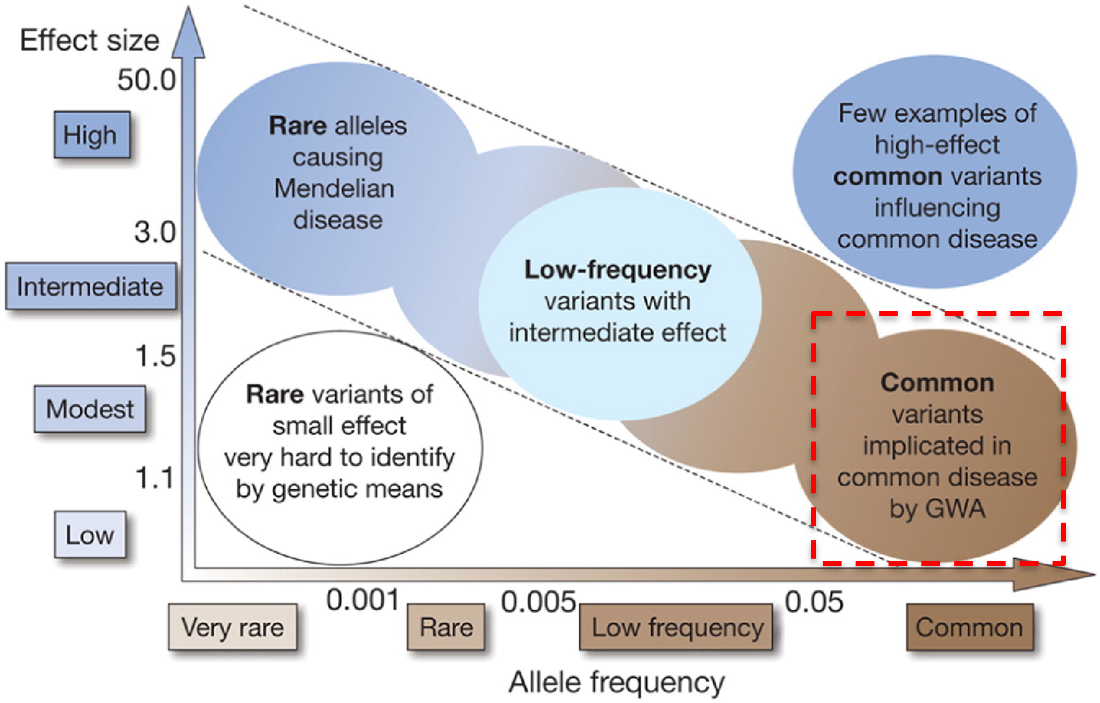
2. GWAS的基本流程和原理

2.1 GWAS的样本选择问题
GWAS常采用case-control的方式研究common disease ，而对于一些常见表型的遗传关联研究则会采用人群队列的方式来进行。当开始一个GWAS分析时，遇到的第一个问题是，试验如何设计？样本如何选择？Cases和Controls的样本该如何设定？
a. Cases和Controls尽量来自于同一个抽样总体，比如说来自亚洲的Cases和来自欧洲的Controls做对照分析就会存在总体分布间的偏差；
b. 无亲缘关系群体，减小群体结构的影响。同上类似，减少除表型因素外其它因素差异引起的干扰；
c. 样本大小需要足够大;
d. 如果是case-control分析，两组样本大量尽量平衡或者controls多于cases，降低假阳性率。

2.2 变异数据质控
当通过SNP芯片检测的方法或者全基因组测序的方法检测所有样本的基因型并进行基因型质量质控后，在进行关联分析前仍需要对数据进行质控预处理，减少干扰因素（比如稀有变异，群体结构等）对后续关联分析的影响。质控条目包括以下几点：
a. 缺失率：包含样本-变异矩阵中，每个样本中变异位点缺失率和每个位点中样本缺失率；
b. 次等位基因频率：过滤掉稀有或低频突变；
c. 杂合度过滤；
d. Hardy-Weinberg平衡过滤。
借助于plink、vcftools, bcftools等工具都可以完成vcf变异数据质控。

2.3 基因型填充
样本-变异矩阵中缺失基因型可以用人群单倍型参考面板推断。可用imputation工具如Impute，minimac。

2.4 群体结构校正
可以通过主成分分析的方式确定群体主要结构成分，可在回归分析时，与其它群体结构变量如年龄，性别等作为协变量处理，去除这些因素的影响。

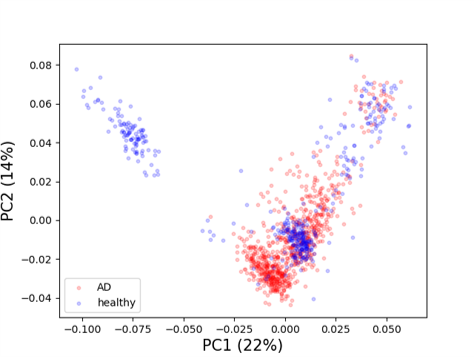
2.5 关联分析
2.5.1 预备知识——假设检验
检验两组数据之间是否存在显著差异。
a. 提出零假设：两组数据间不存在显著差异；
b. 备择假设：两组数据间存在显著差异。
c. 然后可以结合数据和已知参数情况，选择对应的有参检验或非参检验；
d. 若数据差异的P-value小于显著性水平，则说明两组数据间存在显著差异，备择假设成立。
2.5.2 预备知识——卡方检验
卡方检验是有参检验的一种，我们这里采用卡方独立性检验，检验两个变量之间的相关性。
a. 零假设：两个变量独立，不相关；
b. 备择假设：两个变量相关。
c. 在列联表中计算期望水平和观测值之间的差异，构建卡方统计量；
d. 若数据差异的P-value小于显著性水平，则说明两组数据间存在显著差异，备择假设成立。
2.5.3 使用卡方检验进行关联分析
使某一变异位点观测数据如下：考虑一对等位基因A和a，A是主等位基因，a是次等位基因，对应基因型有3种AA, Aa, aa。

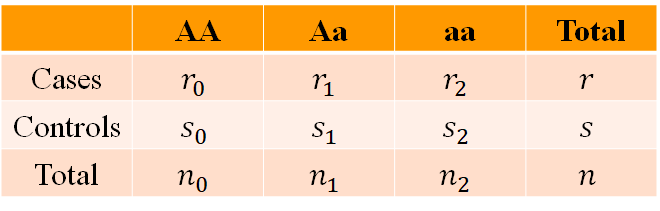
假设患病情况和基因型状态无关，则可对样本进行自由度为2的卡方检验。
也可在allele-level进行检验：

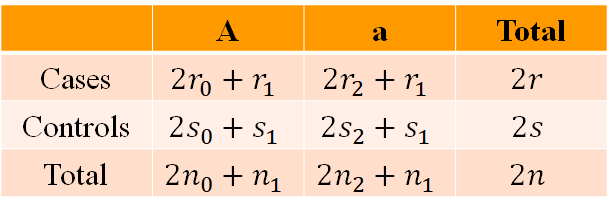
假设患病情况和等位基因状态无关，则可对样本进行自由度为1的卡方检验。

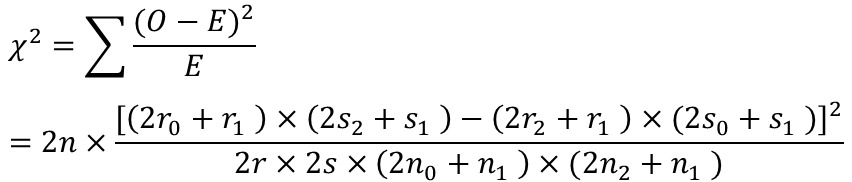
根据卡方检验的P-value大小可在一定显著性水平对假设肯定或否定，从而确定该变异是否与疾病显著相关。
2.6 遗传效应大小的衡量
疾病odds ratio为不同基因型状态或不同等位基因下患病风险的比值。


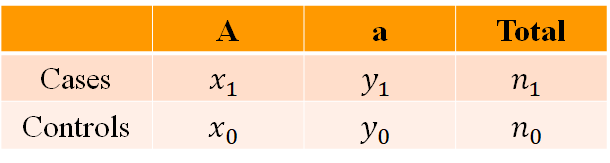
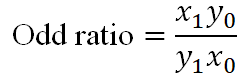
疾病odds ratio反映不同等位基因和疾病的关联程度。
2.7 复杂遗传模型中的关联分析
考虑一对等位基因A和a，A是主等位基因，a是次等位基因，对应基因型有3种AA, Aa, aa。考虑三种情况：
AA和Aa的遗传效应一致（A为显性）；
AA和aa的遗传效应一致，和Aa不一致；
Aa和aa的遗传效应一致（a为隐性）。


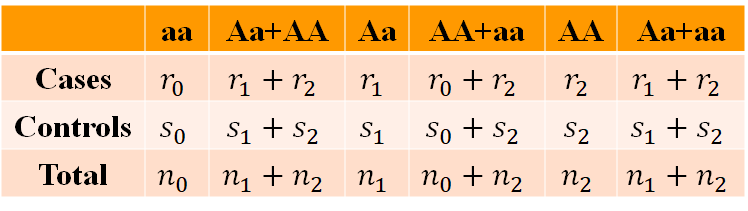
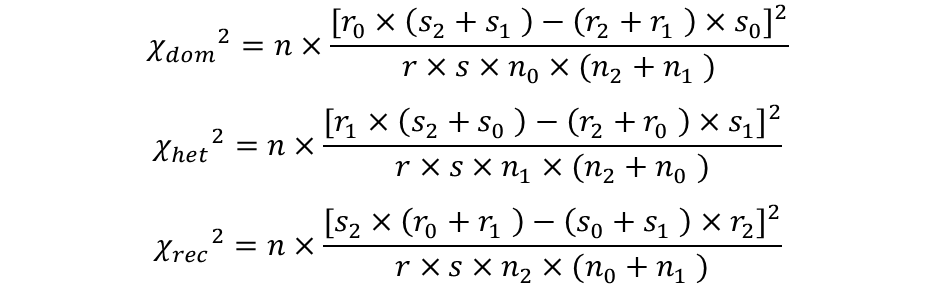
已知疾病或表征是显性遗传，选择显性遗传模型；
已知疾病或表征是隐性遗传，选择隐性遗传模型；
已知疾病或表征具有杂合优势或者杂合劣势的特征，可选择杂合遗传模型；
在无先验的情况下，一般会默认采用共显性模型（也叫加性效应模型）；
在无先验的情况下，也可以采用Cochran–Armitage trend test来检测共显性、显性，隐性或杂合遗传效应。
2.8 检验变异-疾病关联的回归方法
2.8.1 对于连续型性状，可用线性回归方法：

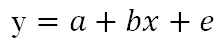
𝑥为观测的基因型，y为对应的表型值，a为截距，b为基因型的效应大小，e为残差项。

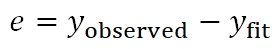
最小化残差项，可得到该等位基因座上基因型和表型的回归方程，从而估计该等位基因座的效应大小b。

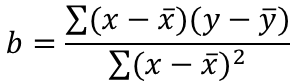
2.8.2 对于二元离散型性状，可用逻辑回归方法：

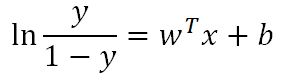
𝑥为观测的基因型，y为对应的表型值，b为截距， 𝑤^𝑇 为遗传效应大小。
用极大似然法求解。
2.9 多重检验校正
原因：每一个等位基因座都会进行一次假设检验，全基因组范围内大量假设检验会引起I类错误扩大和假阳性关联。比如说一次假设检验的假阳性率为0.01，进行100000次假设检验则会出现1000个假阳性结果，总体上假阳性会偏高。
措施：
1）Bonferroni 校正；

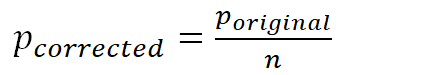
n是检验次数。
若初始显著性阈值设为0.05，校正次数为1000000，则校正后阈值为5×10^(−8)，那么假阳性检出率也会降低1000000 倍，在1000000次检验中出现的次数为0.05。
存在的问题：
阈值设得过于严格，被拒绝的不只是假阳性结果，很多真阳性结果也会被拒绝。目前普遍采用的经验阈值为5×10^(−8)，也可根据需求设定更宽松或更苛刻。
2）FDR（False Discovery Rate） 校正。
原理：将检验中假阳性和真阳性的比例控制在一定范围内。
将n次检验的结果按从小到大排列，令k为每个结果的排名次序；
找到符合原始阈值α的最大k值，满足P(k)<=α×k/m，认为排名从1到k的所有检验存在显著差异；
也可计算对应的校正p值q-value=p×(m/k)检验显著差异结果。
2.10 常用的GWAS工具
Plink https://www.cog-genomics.org/plink/2.0/
GCTA https://cnsgenomics.com/software/gcta/
2.11 后续分析和验证
至此，通过GWAS已经获得了一些高度显著的位点。在关联位点非常多的情况下直接去做实验验证还是不太可行的：
a. 实验/临床验证成本大；
b. 大量common SNP与causal SNP连锁，导致其出现和causal SNP高度相关，因此出现虚高的显著度。
因此，还需要从连锁角度和功能基因组层面分析相关位点的因果性。然后再开展实验验证或临床验证。